ロボットシステムで使われているプロセッサーについてまとめていきます。プロセッサーというと狭義の定義では CPU のみを指すこともありますが、ここでは CPU に加えて、GPU、FPGA、DSP、AI 専用 LSI を取り上げます。まずは各デバイスの名称の意味や簡単な説明に触れてから、具体的な内容へ入っていきます。
CPU は Central Processing Unit の略称で、コンピュータの中核を担います。コンピュータについては「ロボットのコンピュータの概要」と「コンピュータの構成」のページに記載しています。
GPU は Graphics Processing Unit の略称で、パソコンやスマートフォンなどのディスプレイに表示する画像(映像)のデータを作成する役割を担います。近年になって、流体シミュレーションなどの科学技術計算やニューラルネットワークなどの人工知能の計算でも活用されるようになり、ロボットシステムでも広く使われています。
FPGA は Field Programmable Gate Array の略称で「書き換え可能なデジタル回路」という機能を持ちます。FPGA そのものにはプロセッサーとしての機能はありませんが、書き換え可能な部分に CPU 回路を載せたり、CPU の計算の一部を FPGA に肩代わりさせたりすることがあることから、プロセッサーを選定する際に候補として挙げられることがあります。こういった背景から、このサイトではプロセッサーと同列に扱います。
DSP は Digital Signal Processor の略称です。四則演算やフィルタリング処理、FFT などのデジタル値に対する数学的な計算に特化したデバイスです。フィルターの特性を変更できるなど、計算の内容を一定の範囲内で調整できるようになっている点が特徴です。機能を絞っていることから、計算の種類によっては CPU や GPU、FPGA に比べて高速かつ低消費電力で実行することができるため、プロセッサーを選定する際に候補に上がります。
AI 専用 LSI は 2020 年前後から流行り始めたデバイスで、多くはニューラルネットワークの計算を効率的に実行できるような構成になっています。様々なメーカーが多種多様のアーキテクチャを採用しており、王道と言えるようなものはまだ存在しない状況です。
CPU
CPU は「Central Processing Unit(中央演算装置)」の略称で、その名の通りコンピュータの中央に位置し、コンピュータの機能の中核を担う半導体デバイスです。「ロボットのコンピュータの概要」のページで示したコンピュータの定義の図を再掲します。
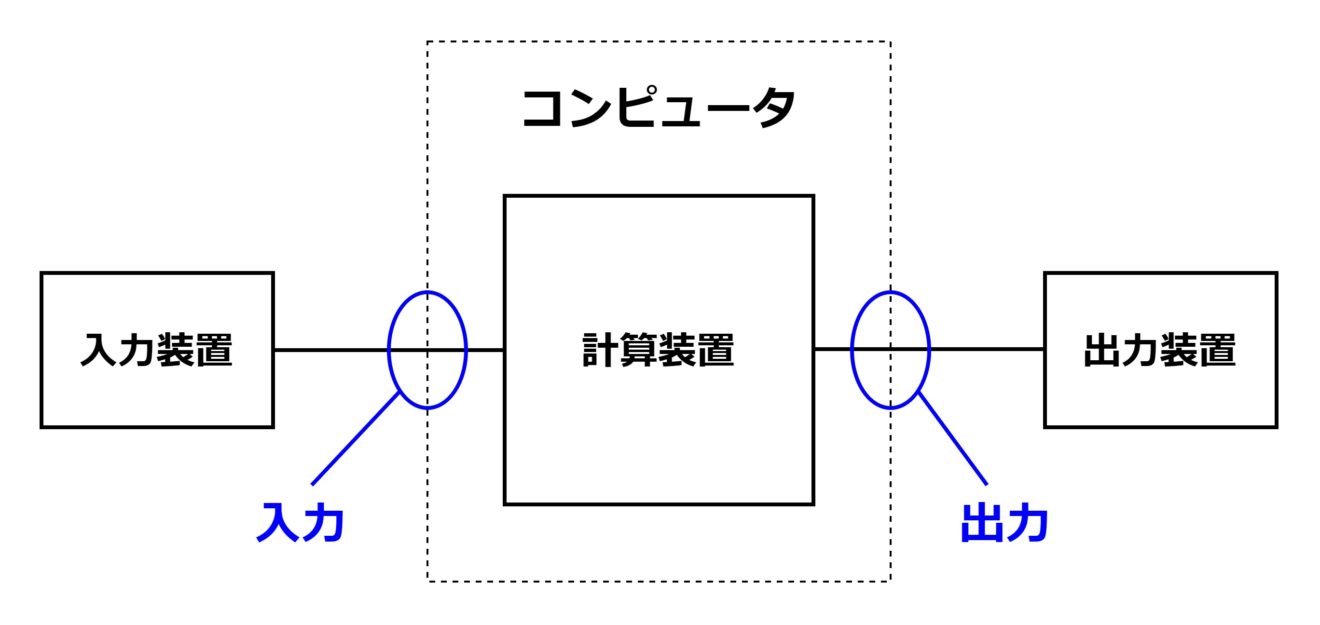
この計算装置にあたるのが CPU です。厳密には DRAM や GPU などの半導体デバイスと組み合わせて計算装置が成り立ちますが、計算装置は CPU 抜きには全く成立せず、その機能の多くが CPU に依存します。ロボット技術の全体像を俯瞰する視点から見ますと、「計算装置≒CPU」と言っても過言ではないでしょう。
CPU の基本的な役割は、OS やアプリケーションソフトウェアを適切かつ効率的に動かすことです。つまり CPU は「ソフトウェアを実行するためのハードウェア」ということになります。アプリケーションソフトウェアには、例えば Excel や Word といったものがあります。一般的なハードウェアは、デジタル回路やアナログ回路、センサー、アクチュエータなどによって構成され、製造した後に形を変えることはできません。そのため、ハードウェアの機能も固定化されます。この話の流れに沿うと、Excel 専用のハードウェアや Word 専用のハードウェアが必要になります。(実際に、パソコンが普及する前は電卓とワープロという個別のハードウェアを使い分けていました。)そうならないように、CPU には1つのハードウェアで様々なソフトウェアを実行できるようにする工夫が施されています。
コンピュータアーキテクチャを開発した先人達は、100 個程度の基本的な処理を組み合わせて様々なソフトウェアが成立するような仕組みを構築しました。コンピュータの世界でこれらの基本的な処理は「命令」と呼ばれ、例えば、加減算、データの読み込みや書き込み、比較演算、条件分岐といった処理が含まれます。100 個程度の命令であれば、1 つのハードウェアで実現することができます。このハードウェアこそが、CPU です。
ソフトウェアは複数の(たくさんの)命令に分解され、CPU で順次実行されます。C 言語などのプログラミング言語で書かれたコードを命令に分解し、CPU が読解可能な機械語というデータ形式に変換することを「コンパイル」と言います。また、コンパイル機能を持ったソフトウェアを「コンパイラ」と呼びます。コンパイラは CPU が処理できる命令の組合せ(「命令セット」と呼びます)を知っている必要がありますので、コンパイラは基本的に は CPU ごとに用意することになります。(CPU を隠蔽する役割を持つ OS を利用する場合には、コンパイラは CPU ごとに用意する必要がなく OS ごとに用意します。)このように、命令セットという約束事を介してコンパイラがソフトウェアと CPU の橋渡しをすることで、Excel も Word も同一のハードウェアで実行することができるというわけです。このあたりのことは「コンピュータの構成」のページにも記載していますので、ご参考ください。
CPU の基本的な構成図は下図のようになっています。
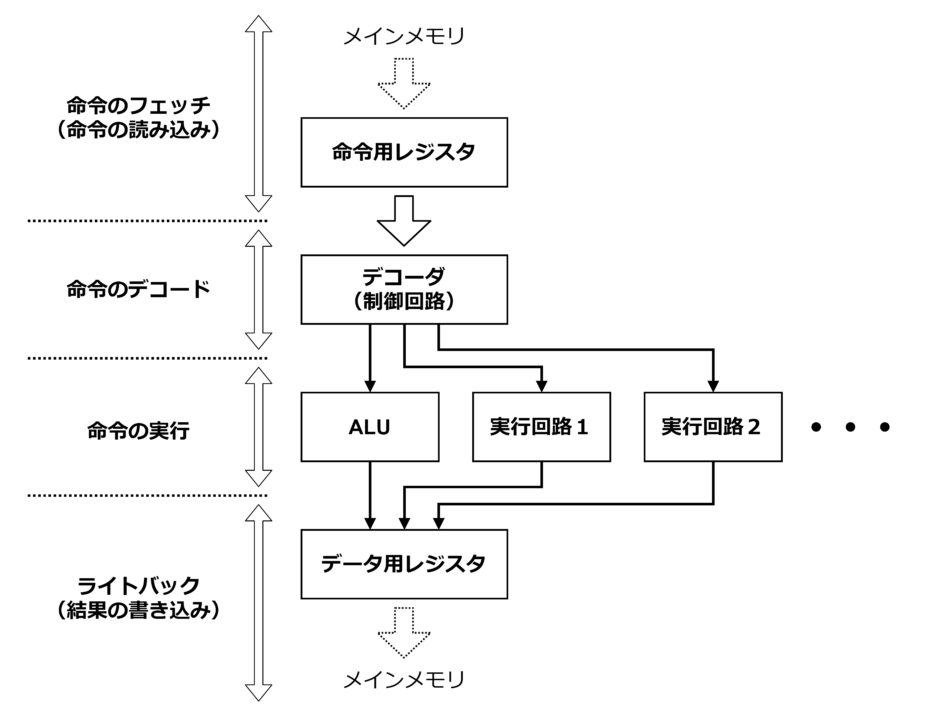
命令のフェッチ
パソコンなどの一般的なコンピュータでは、命令の情報は実行可能な形式(例えば “.exe” 形式)の機械語データとして HDD や SSD といったストレージに格納されています。ソフトウェアを起動すると、データがストレージから DRAM などのメインメモリにコピーされます。そして、命令の情報がメインメモリからCPU へ順次送られていきます。その情報を一旦保存しておくのが「命令用レジスタ」で、この一連の処理を「命令のフェッチ(命令の読み込み)」と言います。
命令のデコード
そして次に、デコーダによって命令の中身をデコードします。デコードという機能は様々な場面で使われますが、ここでは CPU の命令を題材にデコードについて補足しておきます。まずはじめに、4 本の信号線で 4 つの制御信号を作ることを想定するとしましょう。4 つの制御信号の ON/OFF (1/0) の状態は単純には 4 ビットで表現できます。例えば、2 番目の信号線だけを ON するとした場合は “0010”、4 番目だけを ON する場合は “1000” といった感じです。いずれか 1 つの信号を ON するという前提であれば 4 通りの組合せがあるので、4 ビットで表現するというのは自然な流れです。一方で 2 進数の世界を思い返してみると、4 通りの情報は “00” “01” “10” “11” のように 2 ビットで表現できます。2 ビットで表現できる情報に 4 ビットも使うのは冗長です。そういった場合にデータ量を節約するために 4 つの制御信号の情報を 2 ビットのデータに圧縮することを「エンコード」と言います。CPU の命令の情報もエンコードされた状態でストレージやメモリに保管されています。情報を保管する時はデータ量を小さくしておきましょうという発想です。一方でここで掲げている想定では電気的に回路を動かすために 4 つの信号線を ON/OFF しますので、最終的に 4 つの個別の 1/0 の情報が必要になります。そのために 2 ビットで保管していた形式から 4 つの信号線の情報に変換する処理が「デコード」です。そして、デコードを実行するのが「デコーダ」の役割です。
なお、実際の CPU で命令を何ビットで保管しておくかは CPU の種類によって異なります。CPU の種類を「8bit CPU」「32bit CPU」といった言葉で表すことがありますが、たいていはこのビット幅がそのまま命令のビット幅を示します。32bit というと(「\(2^{32} = \) 約 40 億」なので) 100 個前後の命令しかないことに対してだいぶ冗長のように見えますが、命令の中には CPU 内のどのレジスタ(記憶用のデジタル回路)にアクセスするかというアドレス情報も含まれていてけっこうな情報量が必要になり、ビット幅にあまり余裕は無かったりします。
命令の実行
以上のような形でデコーダによって生成された制御信号は「実行回路」へ送られ、命令の内容が実行されます。実行回路の種類は複数ありますが、最も重要な回路は「ALU」です。ALU は、正式名称を「Arithmetic Logic Unit(算術論理演算装置)」と言います。算術演算と論理演算の機能を持ったデジタル回路です。算術演算は、整数型の値の加減算のことを指します。論理演算は、ビットの AND (論理積) や OR (論理和) 、ビットシフト演算のことを指します。複雑なソフトウェアも、実はこういった基本的な演算を組み合わせることで成立しています。ソフトウェアの中では、命令の実行状況に合わせて命令自身や演算対象のデータ(変数データなど)をメインメモリから読み出すということも頻繁になされます。メインメモリに格納されているデータはアドレスで管理されています。アドレスの値も加減算によって計算されますので、ALU の出番はかなり多いです。さらに、プログラミング言語で言うところの if 文の中の比較演算も減算をベースにした処理になり、ALU を使います。
その他の実行回路には、「乗算器」「除算器」「FPU」などが挙げられます。乗算器は、整数の掛け算を実行するデジタル回路です。デジタル回路の入門書に書かれている通り、整数の掛け算は整数の足し算とビットシフト演算の組み合わせで実行することができます。つまり、ALU を複数回実行すれば掛け算の結果を得ることができます。しかし、そのためには ALU を何十回や何百回も動かさないといけません。つまり、たくさんのクロックサイクルが必要となります。また、掛け算を実行している間 ALU を占有してしまうため、パイプライン処理(後述)などを使った効率的な命令の実行がしづらくなります。CPU の処理速度が多少遅くても良いケースであれば問題になりませんが、パソコンやスマートフォンなど処理速度が求められる製品や、ロボットの認識や判断などの複雑な演算を伴う機能にとっては不十分とみなされます。そういった場合には、ALU とは別に乗算器を用意しておきます。別の回路になりますので高速化の処理をしやすくなりますし、掛け算に特化した回路構成にすることで少ないクロックサイクルで掛け算を実行できるようになります。
除算器も、乗算器と同じような理由で個別に用意することがあります。ただし、除算の計算手順は乗算と比べてやや複雑です。小学校で習った割り算のひっ算のように、除算では商が確定するまで何度も掛け算と引き算を繰り返します。デジタル回路では 2 進数を計算対象としますが、手順は 10 進数と変わりません。これは「再帰的な処理」となり、回路内にフィードバックの経路が必要になります。原理的には、掛け算、引き算、比較演算の組合せになることから ALU と乗算器を組み合わせることで除算は実現できますし、ALU 単独でも演算可能です。それでも除算を高速に実行したいというニーズがある場合には、専用のデジタル回路として除算器を搭載します。なお、ソフトウェア開発の世界では「割り算は演算コストが大きいことから出来るだけ避けるべき」と言われています。全てのケースで対応できるわけではありませんが、割り算を掛け算で代替できるようにしたり、2 の累乗(\(2^n\))の割り算で表現できるようにしておいて ALU のシフト演算で処理するように仕向けたりと工夫をするのが一般的です。そのため、用途によっては除算器のニーズは結果的に小さくなり、CPU に搭載されないことも多いようです。
FPU は正式名称を「Floating Point Unit(浮動小数点演算装置)」と言います。浮動小数点は、例えば「\(3.25 \times 10^5\)」や「\(5.3 \times 10^{-3}\)」のように表記され、小数点の位置をダイナミックに変更できる数値の型(表現方法)のことを指します。2 進数の場合には、例えば「\((1.101)_2 \times 2^{(1011)_2}\) 」のような表現になります。「\(A \times 10^B\)」とした場合に \(A\) を仮数(部)と呼び、\(B\) を指数(部)と呼びます。(2進数の場合は \(1.101\) の \(1.\) を除いた \(101\) が仮数にあたります。)浮動小数点には、指数部を用意して \(A\) と \(B\) の 2 つの数値で 1 つの値を構成することで、整数に比べて同じ情報量で表現できる値の範囲を劇的に広くとることができるという特徴があります。浮動小数点を使うことで、例えば、ボルツマン定数 \(k = 1.38 \times 10^{-23}\) と物質の温度 \(T = 6 \times 10^3\) の掛け算(\(k \times T\))のように桁の異なる数値同士を演算することが可能になります。これを整数型だけで表現しようとすると 100 ビット近いサイズの ALU が必要になり、対応するハードウェアを作るのがとても大変になってしまいます。
FPU は浮動小数点型の値同士の加減乗除の演算や比較演算を可能にするデジタル回路です。CPU によっては平方根の計算に対応する FPU が搭載されていることもあります。浮動小数点の演算は、1 つの値を仮数部と指数部という 2 つの値で表現していますので、通常の整数の計算手順とは大きく異なります。例えば「\(3.25 \times 10^5\)」と「\(5.3 \times 10^{-3}\)」という 2 つの値の計算を仮定します。掛け算はわりと単純で、仮数部同士を掛け算して、指数部同士を足し算します。つまり、\(3.25 \times 5.3 = 17.225\) と \(5 + (-3) = 2\) で計算結果は \(17.225 \times 10^2\) となります。最後に仮数部の小数点の位置を整理して、\(1.7225 \times 10^3\) となります。なお、実際の計算は 2 進数になりますが、イメージしやすくするために慣れ親しんだ 10 進数を例にしていますのでご了承ください。
次に足し算を考えてみます。指数部が異なるとそのまま足し算できませんので、はじめに指数部を揃えるという処理をします。例えば \(3.25 \times 10^5 = 325000000 \times 10^{-3}\) のような形です。そして、仮数部同士を足し算します。つまり、\(325000000 + 5.3 = 325000005.3\) です。最後に小数点の位置を整え、\(3.250000053 \times 10^5\) となります。
以上のように整数の演算とは全く異なります。これらの計算は原理的には ALU 単独でも実行可能ですが、浮動小数点の演算スピードを高めたい場合には FPU という専用のデジタル回路を別途用意します。ただし、浮動小数点の演算の過程からも想像できるように、FPU は ALU と比べて大きなデジタル回路になることが多く、必然的に CPU のチップ面積も大きくなってしまうというデメリットがあります。そのため、低消費電力や低価格を謳っているコンパクトな CPU(MPU や MCU とも呼ばれたりする)には FPU が搭載されていないこともあります。
結果の書き込み
実行回路で演算した結果は「データ用レジスタ」に書き込んで保存します。結果をレジスタに書き込むことを「ライトバック」と呼ぶこともあります。演算結果を次の命令ですぐに使う場合には CPU 内のレジスタにとどめておき、当分使わなさそうならメインメモリへ送ります。レジスタは実行回路の近くにありますし、CPU のクロック速度で動作可能なデジタル回路になっていますので、高速でデータの読み書きが可能です。一方で、メインメモリは一般的に DRAM で構成されていて、通常は CPU とは別の半導体チップになります。データ用レジスタから DRAM に書き込むには一旦チップの外に出る必要があるため、書き込み速度は遅くなります。(読み込み速度も遅いです。)また、DRAM はコンデンサー(容量素子)に受動的に電荷を貯めるという物理的な性質上、DRAM の各セルからの読み込み速度は速くありませんので、その分さらに遅くなります。このように CPU の内部レジスタとメインメモリでは読み書きの速度が圧倒的に内部レジスタの方が速いので、出来るだけレジスタにデータを保持しておいて、あふれた分をメインメモリへ転送するという処理を行ないます。
一方で実際の CPU 製品には、レジスタとメインメモリの間に「キャッシュ」と呼ばれる一時的な記憶領域を実装しておくことがあります。キャッシュは CPU と同じ半導体チップ上に配置され、通常は SRAM で構成されています。SRAM はレジスタほどは速くないですが、レジスタよりも物理的なサイズ(チップ上の実装面積)が小さいことから、SRAM を使うとレジスタよりも大きなデータ容量を確保することが可能になります。とはいえ DRAM よりもビットあたりの物理的なサイズがだいぶ大きくなりますので、チップ上に GB(ギガバイト)オーダーの容量を用意することは困難です。そういった背景から、キャッシュには、最近の命令で使われたことがあってまた近いうちに呼び出されそうなデータを優先的に保存するという方針がとられます。(前出の図ではキャッシュの存在は省略しています。)
パイプライン処理
以上のように、CPU では「命令の読み込み(フェッチ)」「命令のデコード」「命令の実行」「ライトバック(結果の書き込み)」の順に処理がなされていきます。前出の図に示したように、これらの工程はそれぞれ別々の回路で順番に実行されます。つまり、動いている回路は1つだけで、他の3つは待機状態になっています。これではもったいないので、回路を待機状態にする時間を減らして、出来るだけ多くの回路が稼働している状態にするために「パイプライン処理」がなされるのが一般的です。
パイプライン処理は、1つの命令に対してフェッチの処理が終わってデコーダ回路へデータを渡したら、デコード、実行、ライトバックの一連の処理が終わるのを待たずに次の命令のフェッチを受け付ける、という仕組みです。デコーダも、1つの命令の処理が終わり次第、次のデータを受け付け、実行回路と結果用レジスタも同様の動きをします。パイプラインの有無で処理の流れを比較した図を下記に示します。
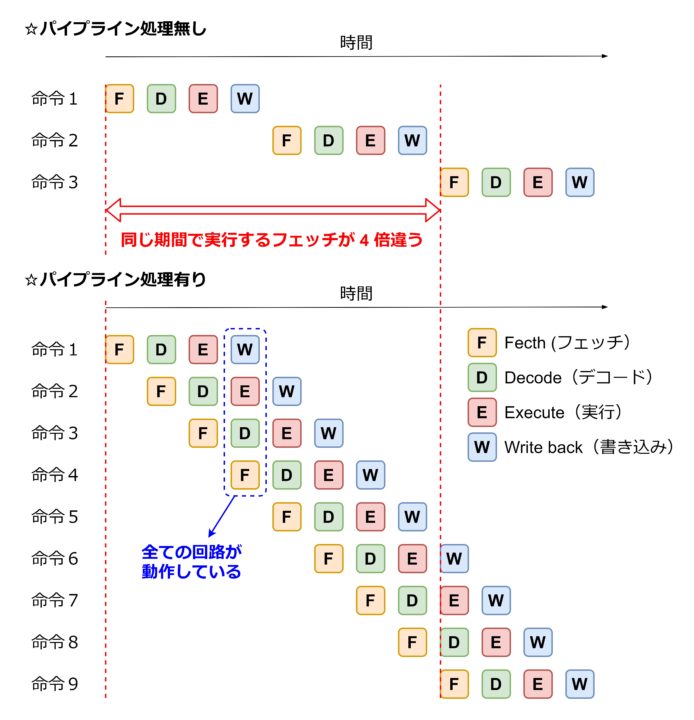
この図では、パイプライン処理を採用することで一定の期間あたりに実行できる命令の数を 4 倍に増やすことが出来ています。(実際にはそこまで効率が上がるとは限りません。)多くの CPU では、このようにパイプライン処理を取り入れ、処理性能を向上させています。
分岐予測
パイプライン処理は、分岐の無い単純なプログラムではうまく効率を上げることができるのですが、if 文などの分岐を含むプログラムではあまり効率を上げることができません。次のようなプログラムコードを例に考えてみます。
if ( a < b ) {
c = w0 * a;
} else {
c = w1 * a;
}
sum = a + b;
out = b + c;コードの中の c の値が条件によって変わります。if の条件式が真 (1) なら a に w0 を掛け、偽 (0) なら w1 を掛けます。そして、最終的な出力 out は c の値に依存するという形になっています。この処理を下図のように命令単位で表現してみます。なお、実際のアセンブリ言語や機械語ではコードの 1 行は複数の命令で構成されることが多いので、リアルではない簡略化したイメージ図だと思ってください。
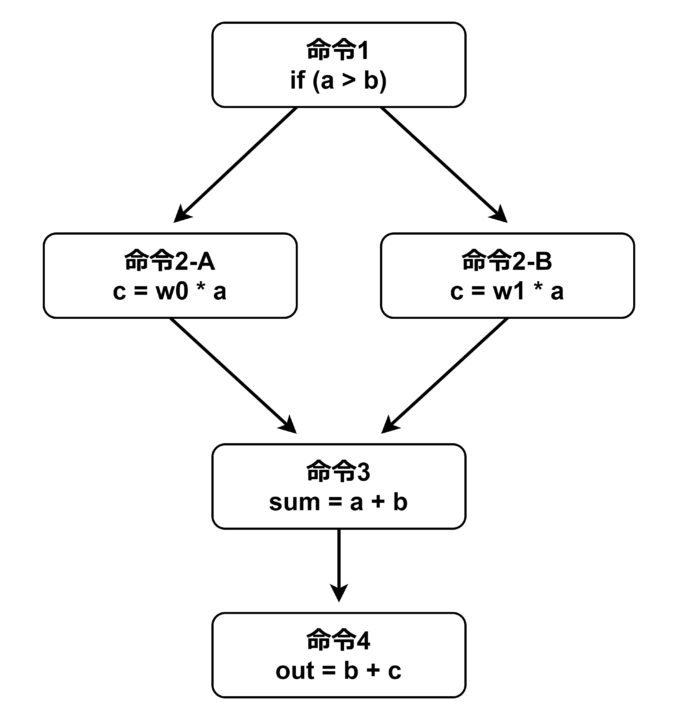
※実際とは異なるので注意
ここで「命令2-A」と「命令2-B」は「命令1」の結果によってどちらが実行されるかが決まりますので、「命令1」の計算が完了するまで開始することができません。つまり、「命令1」の結果の書き込み(Write back)が完了するまで「命令2-A」「命令2-B」のフェッチへ進むことができません。この間、パイプライン処理が機能せず、効率化の効果が薄れてしまいます(下図)。
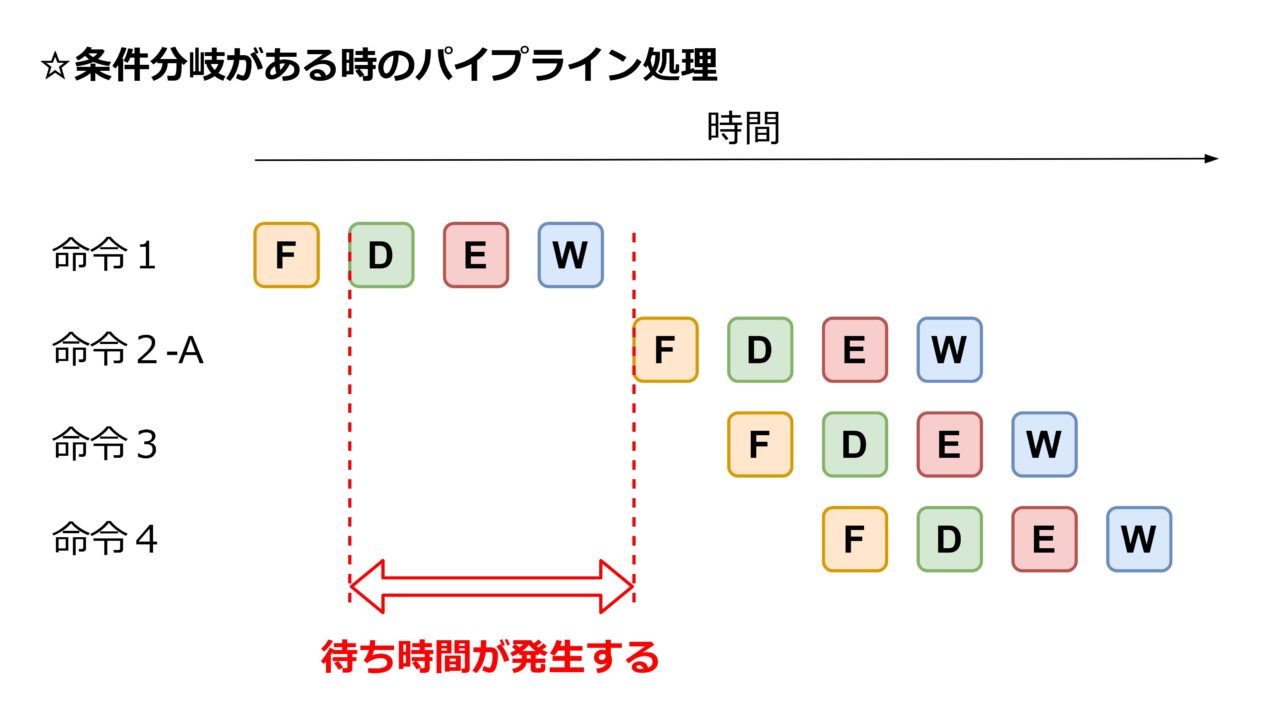
そこで登場するのが「分岐予測」です。分岐予測は、どちらの分岐に進むかを予測して、思い切ってパイプライン処理を進めてしまうという機能です。前出の例で言うと、a < b になると予測する、あるいは「命令 2-A」へ進むと予測する、ということに相当します。実際に予測通りにプログラムが進むかどうかは分かりせんので博打を打つことになります。予測が外れれば博打に負けたことになり、もう一方の分岐の命令を始めからやり直すことになります。博打という意味合いで「投機実行」と呼ばれることもあります。
一見、無謀な挑戦に見えますが、実は分岐の仕方にはある程度偏りがあってランダムではないことから、けっこう成功率が高くなります。CPU とプログラムの組み合わせによって変わりますが、成功率は 90% 程度のようです。これはパイプライン処理の効率をほぼ維持できることを意味します。
分岐予測の仕方は色々な方法があるようです。一般的なプログラムコードを実行した時にどちらの命令へ進むことが多いかを統計的に分析して可能性の高い方へ進むように分岐予測の回路を作っておいたり、実行されている命令の状況をモニターしてダイナミックに予測を変更する機能を持った回路にしたりと、様々なアルゴリズムとアーキテクチャが考案され、実装されています。
分岐予測を採用することはメリットの方が大きいのですが、デメリットも存在します。まず、下図のように専用の回路を追加する必要があって半導体チップ内の実装面積や消費電力が大きくなるということです。
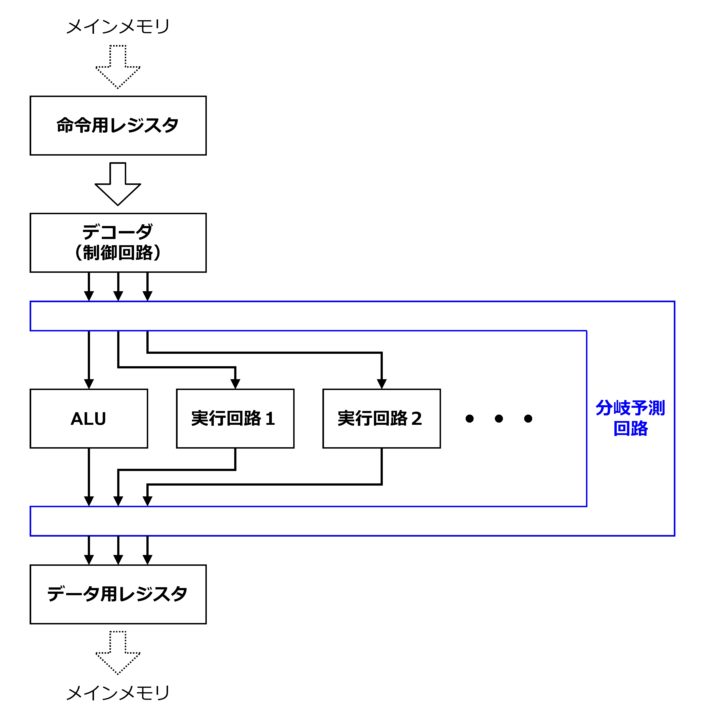
また、分岐予測の処理に多少時間がかかる(クロックサイクルを要する)という点です。例えばランダムなデータを扱うプログラムなど、予測の成功率が低くなるようなケースでは、パイプライン処理の効果が得られず、分岐予測が無い状態よりも演算性能が悪くなることもありえます。つまり、分岐予測には処理時間のオーバーヘッドもあるということを認識しておく必要があります。いずれにしても、パイプライン処理を十分生かすためには分岐の少ないプログラムコードが望ましいとされています。
割り込み
コンピュータは CPU に様々なデバイスを組み合わせて構成します。例えば、一般的なパソコンであれば、USB でマウスやキーボードを接続したり、HDMI で液晶ディスプレイを接続したりします。例えばマウスは、人間が操作をすると画面上のポインタが動いたり、クリックによって画面上のアプリケーションが実行されたりします。
パソコンでは、Web ブラウザ、Excel、ゲームなどのアプリケーションを同時に起動することもあります。多くのソフトを動かすほど CPU の稼働率が上がって個別の処理が遅くなっていきます。この状態では、マウスを動かしてもポインタがすぐに動かず、例えば 1 秒後に動き始めるというような現象が起きてもおかしくありません。しかし、実際のパソコンではそういったひどい状況はほとんど起きません。これは、マウスなどの外部機器からの信号を「割り込み」という扱いをして、優先的に処理を実行するような仕組みになっているからです。CPU は様々なデバイスと接続することを前提に存在していますので、割り込み処理に対応できるように構成されています。
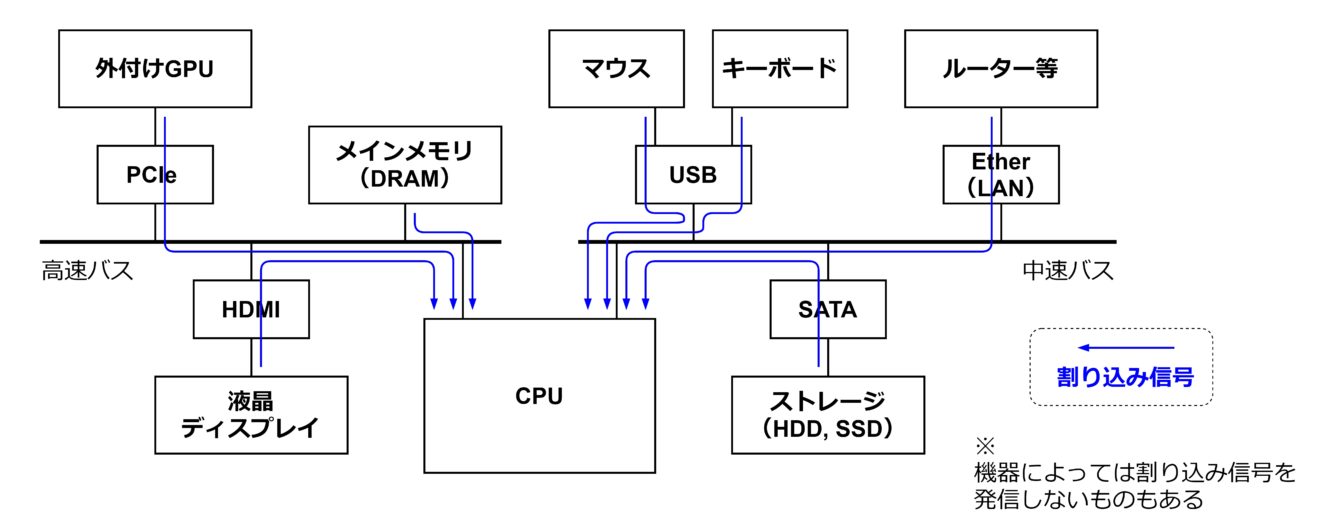
マウスやキーボードなどの機器は「バス」と呼ばれる通信経路に接続されます。このバスを通して各機器から「割り込み信号」が CPU へ送られます。CPU がその信号を受け取ると、実行中の命令を途中で止めて、これから実行しようとしていた命令を保留にします。そして、割り込み信号を発信した一連の命令を優先して実行します。これらの割り込み処理を実行するためには、保留にした命令のデータを一時的に保管するレジスタや、保管を実行する回路が必要になります。その分だけ演算性能が落ちるなどのデメリットもありますが、コンピュータに最低限の操作性を与えるために重要な機能と考えられ、割り込みの機能は多くの CPU に実装されています。参考として、バスを介した接続と割り込み信号のイメージ図を下記に示します。(あくまでイメージで、表現が不正確な部分もありますのでご了承ください。)
GPU
GPU は正式名称を「Graphics Processing Unit」と言い、最終的にディスプレイに表示する画像データを効率的に生成するためのプロセッサーです。その名の通り、グラフィック処理を得意としています。GPU は、例えば Windows PC で複数のアプリケーションを実行して複数のウィンドウを立ち上げた時に、奥のウィンドウは手前のウィンドウに隠れて一部が表示されなかったりする計算をしたり、視覚的に分かりやすくするために手前のウィンドウの境界部分に影がつけてたりする処理を行います。GPU はこのような視覚的な効果の計算を実行し、最終的にディスプレイの各ピクセルの RGB 値を決定するという役割を担います。
GPU が特に力を発揮するアプリケーションの代表例として、3D CG を利用したゲームが挙げられます。ゲームの中のキャラクターや障害物は基本的には 3D のポリゴン(多角形)で表現されます。これらのポリゴンデータが、ユーザーの視点からどのように見えるのかを計算し、最終的にディスプレーに表示する 2D の画素データを作成する必要があります。さらに、ポリゴンの各面に色を付けたり、太陽光や灯りからの光の反射の効果を付けたり、影を描いたりすることで、迫力のある CG 映像になります。これらの計算をしてくれるのが GPU です。
こういったグラフィックの計算は、基本的には行列の計算で構成されます。例えば、3次元空間上のある \((x_0, y_0, z_0)\) を X 軸に沿って \(\theta\) だけ回転させた点 \((x_1, y_1, z_1)\) は次のような数式で表現されます。
$$\begin{pmatrix}
x_1 \\
y_1 \\
z_1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & cos\theta & -sin\theta \\
0 & sin\theta & \cos\theta \\
\end{pmatrix}
\begin{pmatrix}
x_0 \\
y_0 \\
z_0
\end{pmatrix}$$
ポリゴンデータを回転させる際には、ポリゴンの全ての頂点座標に対して、この計算を実行します。次に、このような 3×3 の行列と 1×3 の行列の掛け算を一般化して表現してみます。
$$\begin{pmatrix}
x_1 \\
y_1 \\
z_1
\end{pmatrix}=
\begin{pmatrix}
A_0 & B_0 & C_0\\
A_1 & B_1 & C_1\\
A_2 & B_2 & C_2\\
\end{pmatrix}
\begin{pmatrix}
x_0 \\
y_0 \\
z_0
\end{pmatrix}$$
そして、これを連立方程式の形で表現すると次のようになります。
$$
\begin{eqnarray}
x_1 &=& A_0 \cdot x_0 + B_0 \cdot y_0 + C_0 \cdot z_0\\
y_1 &=& A_1 \cdot x_0 + B_1 \cdot y_0 + C_1 \cdot z_0\\
z_1 &=& A_2 \cdot x_0 + B_2 \cdot y_0 + C_2 \cdot z_0
\end{eqnarray}
$$
それぞれの数式の中身は「掛けて足す」形になっていています。このように掛け算と足し算を組み合わせた演算のことを「積和演算」と呼びます。つまり、グラフィックの計算の基本要素は積和演算であり、GPU は積和演算の実行を得意とするプロセッサーということになります。積和演算自体は CPU でも実行可能で、昔は CPU でグラフィックの計算も実行していました。しかし、年々グラフィックの計算のボリュームが増えていくにつれて CPU の演算リソースを圧迫するようになり、グラフィックの計算を GPU に任せるようになりました。コンピュータシステム全体では、新しい回路を用意してでも CPU と GPU で役割分担するのが効率的と考えるのが主流となり、実際の製品開発にもそういった考えが反映されるようになったようです。
大量の積和演算の実行を必要とするのはグラフィック処理に限りません。ディープラーニング等の AI の計算でも積和演算が主体とすることが多く、GPU が使われることがあります。例えば、画像認識用の AI で用いられる CNN (Convolutional Neural Network) と呼ばれる計算アルゴリズムは「畳み込み層 (Convolution Layer)」と「全結合層 (Fully connected layer)」という基本的な計算アルゴリズムの組合せで構成されます。畳み込み層も全結合層もさらに細かく分解していくと行列の計算や積和演算に行きつきます。つまり、GPU との相性が良いのです。AI の内容によっては一般的なグラフィック処理よりも計算ボリュームが大きくなることも多く、GPU の重要性はますます高くなります。なお、ディープラーニング等の機械学習では、AI の実行を「推論」と呼び、大量のデータを使って推論が適切に機能するように AI 内のパラメータを変更することを「学習」と呼びます。前述の説明は推論をイメージしたもので学習のフェーズでは計算アルゴリズムが異なりますが、基本的には行列や積和演算が大部分を占めることには変わりありません。
GPU の構成
GPU は掛け算や足し算の計算を「並列に」実行することで、グラフィックや AI の処理時間を短縮します。前出の連立方程式を思い出してください。\(x_1, y_1, z_1\) を算出するための 3 つの式がありました。これらの式はどの順番でも計算可能で、互いに因果関係はありません。よって、並列実行が可能です。グラフィックの計算や CNN のような形を持った AI の計算には、互いに因果関係を持たずにどの順番で実行しても良いような数式が大量に含まれるため、かなりの部分を並列に実行でき、大幅な高速化が可能となります。
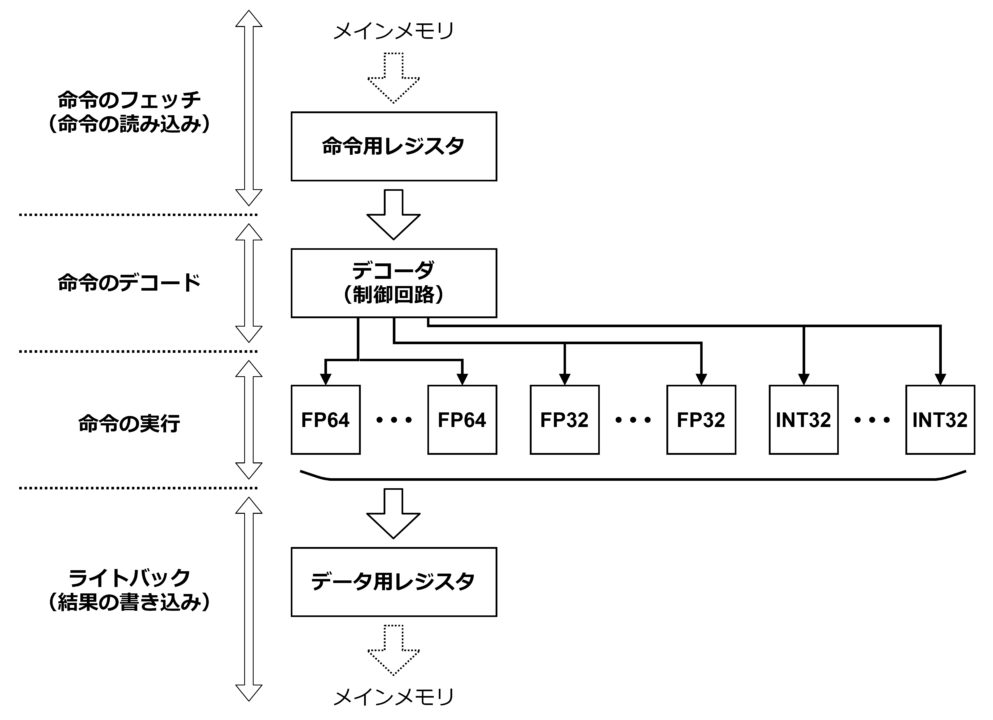
上図は GPU の構成図です。基本的な形は CPU と似ています。GPU も CPU と同様に、命令データを受け取ってデコードし、命令の中身に基づいて演算回路を指定して演算を実行して結果を保存する、という流れになります。GPU の処理内容もプログラムによって記述され、コンパイルによって命令データを含む機械語に変換されます。大枠はほとんど CPU と同じです。GPU 特有なのは同種の演算回路が複数個並列に実装されているところです。この回路構成によって並列演算を実現しています。
FP64 は 64bit の浮動小数点演算器を表現しています。FP32 は 32bit の浮動小数点演算器です。INT32 は 32bit の整数型の演算器です。いずれも掛け算や足し算の演算に対応しています。グラフィックの計算は基本的に浮動小数点型になり、演算器も浮動小数点がメインになります。一方で、行列計算とは別にプログラムの中にカウンタなどの整数演算を含めることもあり、整数型の演算器も用意することが多いです。
64bit の浮動小数点演算は 32bit の計算よりも重いので回路規模も大きくなります。そのため、FP64 は FP32 よりも並列に搭載する回路の個数を少なくする傾向にあります。(GPU 製品によって変わります。)また、同じ bit 幅では浮動小数点演算の回路は整数演算の回路よりも大きくなりますが、INT32 を FP32 よりも多く実装するとは限りません。FP32 を計算の主体に据えた場合には並列数の上限は FP32 の個数に設定するのが妥当で、INT32 の個数もその上限に合わせて FP32 と同じ個数にするとバランスが良くなります。
GPU の大きな特徴は、同一の命令を複数の演算器に伝達する点です。各演算器には別々の計算対象のデータ(変数の値など)が入力されますので、1 度に複数の計算を並列に実行することができます。このような処理の仕方を「SIMD (Single Instruction Multiple Data)」と呼びます。例えば FP32 が 10 個実装されていれば、1 度に 10 個の計算を実行します。これは、処理スピードが単純計算で 10 倍になることを意味します。製品によって異なりますが GPU には同種の演算器が数千個オーダーで実装されていることもあり、同種の演算器が 1 個しか載っていない CPU と比べると極めて高い演算性能を秘めています。CPU にも様々な種類のものがあり、演算器の個数だけでは最終的な性能が決まらないこともありますので一概には言えませんが、GPU は CPU に比べて積和演算を 100 倍程度の速度で実行できることはザラです。
ただし、GPU で並列に実行できるのは、同一の命令の同種の演算器のみです。1 度の命令で、FP32 と INT32 を同時に実行することはできません。そのため、GPU が CPU に比べて有利なのは行列演算のように同種の演算が複数個並んでいるケースのみです。Windows や Linux 等の OS や Web ブラウザ等の一般的なアプリケーションソフトウェアでは、行列演算がメインにはなりませんので GPU が有利にはなりません。また、演算性能が高いといっても、1回の計算にかかる時間が短くなる訳ではありませんので、命令を開始してから結果が出てくるまでの待ち時間は変わらない点も注意が必要です。(スループットは高いですが、レイテンシーが低く抑えられる訳ではありません。)以上のことから言えるのは、GPU が力を発揮するのは、同種の演算を並列かつ大量に実行する時だけだということです。
GPU と CPU の違い
GPU は CPU と同じように命令を順次実行する装置になっていて、CPU と同様にプロセッサーと呼ばれますが、大きく異なる点もあります。第一に GPU には、CPU に搭載されている分岐予測の機能がありません。分岐に対応した仕組みは持っていますが、極めて貧弱です。一般的なソフトウェアには多くの分岐が含まれるため、分岐予測が無いとパイプライン処理による高速化がほとんど機能しません。この点から、OS やアプリケーションソフトウェアを GPU で実行するのは現実的とは言えません。
第二に GPU には、外部からの割り込み信号に対応する機能がありません。コンピュータは、プロセッサーに入力装置、出力装置、通信装置を組み合わせて構成することが前提であり、これらの装置は割り込み処理を必要とします。GPU にも、実行する命令の優先順位を変更するという割り込みの機能はありますが、外部の装置からの割り込み信号への対応能力とは別物です。そのため、GPU のみでコンピュータを構成することはできません。
以上の 2 つの機能が GPU に無いことから、GPU を単独で使用することはまずありません。基本的には CPU と一緒に使います。基本的なソフトウェアの処理は CPU が担当し、大量の単純計算を GPU に任せる、という役割分担をします。CPU に GPU を付加することで計算を高速化できることから、GPU を「CPU のアクセラレータ」と呼ぶこともあります。
GPU の実装(利用)方法
GPU をどのように実装して利用するか、その方法にはいくつかのパターンがあります。下図に、代表的な3つの実装(利用)パターンを示します。前述の通り、GPU は CPU と合わせて使いますので、CPU との関係性に注目して描いています。
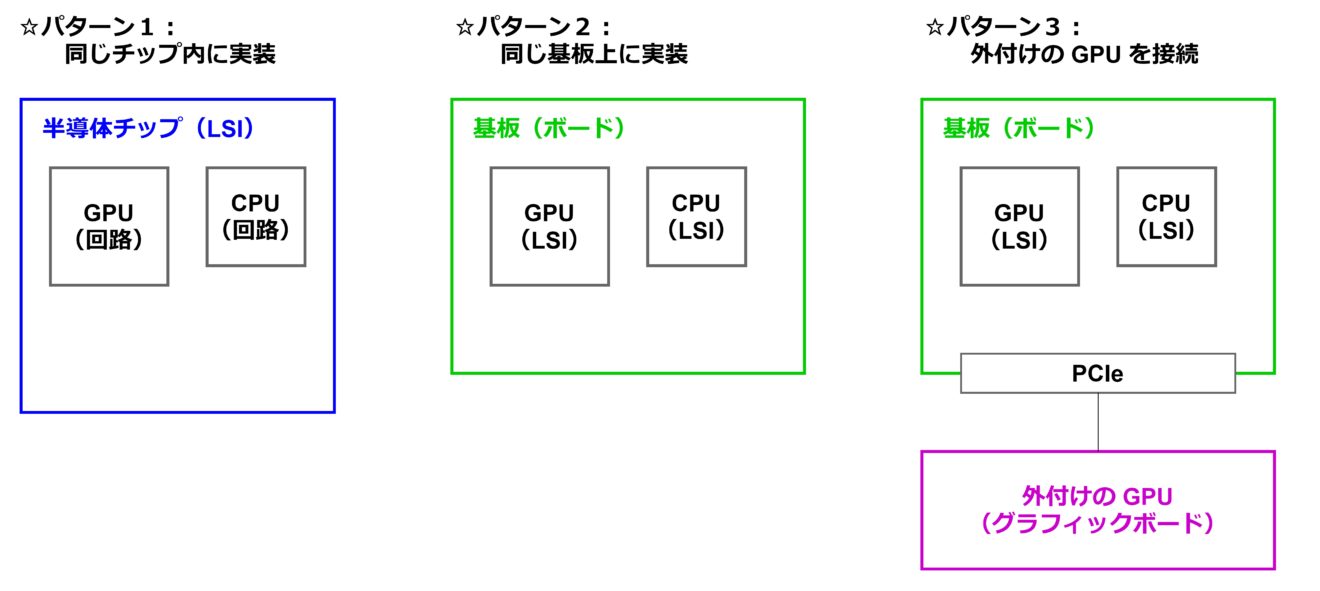
1つ目は GPU と CPU を1つの半導体チップ(LSI)の中に実装するパターンです(パターン1)。スマートフォンや比較的コンパクトなパソコンなど、最終製品のサイズを小さくすることを優先する場合に採用される形式です。また、NVIDIA 社の Jetson シリーズなどの人工知能向けのコンピュータもこの形式になっています。2つ目は、GPU と CPU をそれぞれ別の半導体チップとして作っておき、基板(ボード)上で接続するというパターンです。パソコンや PlayStation といった専用のゲーム機で採用されています。
3つ目は、CPU と GPU が載っているボード(マザーボード)に PCIe(PCI-Express)などのインターフェースで外付けの GPU(グラフィックボード)を接続するというパターンです。CPU と GPU が載っているボードはパソコンやサーバーに相当します。元々用意されている GPU では演算性能が物足りない場合に利用される形式で、グラフィック処理が重いパソコンゲーム、3D CAD、ディープラーニングといった用途で使われます。なお、ボード上の CPU と GPU は(図の通り)別々の半導体チップになっていることもありますし、1つの半導体チップにまとめられていることもあります。
ロボットシステムに GPU を利用する場合にはどのパターンも選択肢としてありえますが、基本的にはエッジ側ではパターン1、サーバー側ではパターン3が有力な選択肢になるでしょう。
DSP
DSP は正式名称を「Digital Signal Processor」と言い、デジタル信号処理に特化したプロセッサーです。センサーから出力される時系列データの信号処理によく使われます。DSP を使った典型的なシステム構成図を下記に示します。

名前の通り、プロセッサーの一種で、CPU や GPU と同様に命令を順次実行していくことで演算の目的を果たします。実行回路に整数や浮動小数点の演算器が含まれる点も同様ですが、計算の用途を絞っている点が異なります。DSP が対応する主な計算は「デジタルフィルタ」「FFT」「三角関数」「音声のコーデック」です。これらの計算を低消費電力で高速に実行できるように演算器がチューニングされています。
CPU や GPU でもデジタルフィルタや FFT の計算は可能ですが、これらのプロセッサーは DSP に比べて汎用性が高い分だけ処理時間や消費電力のオーバーヘッドも大きくなります。決まった計算を定常的に実行し続けるのであれば、DSP を採用すべきでしょう。
なお、CPU と DSP が1つの半導体チップに搭載されているマイコン製品も多数存在します。時系列データを処理するシステムを作る際には、DSP 単体の半導体製品と CPU と一体化した半導体製品の両方を選択肢に入れて検討することが必要です。
FPGA
FPGA は正式名称を「Field Programmable Gate Array」と言い、「書き換え可能なデジタル回路」という機能を持つ半導体デバイスです。「Programmable」が書き換え可能という意味に相当し、「Gate Array」はデジタル回路の要素が並んでいる様子を表現しています(FPGA の構成については後述)。「Field」は「現場で」という意味で、わざわざ工場に持ち込まなくても技術者が自分で機能を書き換えることができる、というニュアンスを表しています。
LSI 内の一般的なデジタル回路は、AND や OR といった要素回路から成る「組合せ回路」とメモリー機能を持つ「D 型フリップフロップ回路(DFF)」で構成されます。イメージは下図の通りです。
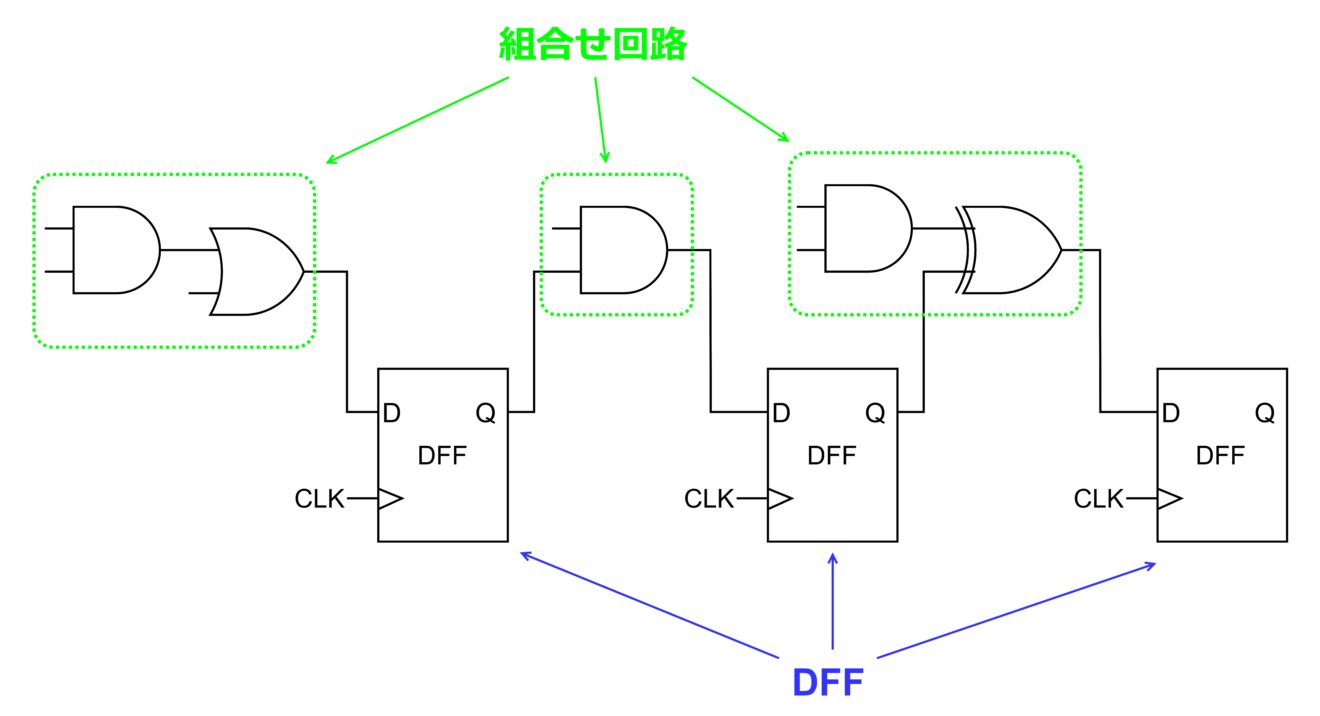
デジタル回路を作る際には、組合せ回路や DFF などの要素回路を物理的に配置して、それらをメタル配線で物理的に接続します。物理的に作り込むため、1度作った後に変更することはできません。(FIB 加工などの特殊な加工を行えば少しだけ変更することもできますが、かなりのコストがかかる上に変更できる部分が極めて少ないため、日常的には行うのは困難です。)FPGA は、本来変更できるはずがないデジタル回路があたかも書き変わったかのように振舞わせる機能を持ちます。
FPGA の構成
デジタル回路の機能は、組合せ回路の機能(真理値表)と DFF との配線で大よそ決まります。つまり、組合せ回路の真理値表と配線経路を変更できれば、デジタル回路の機能が変更できたことになります。変更箇所のイメージを下図に示します。
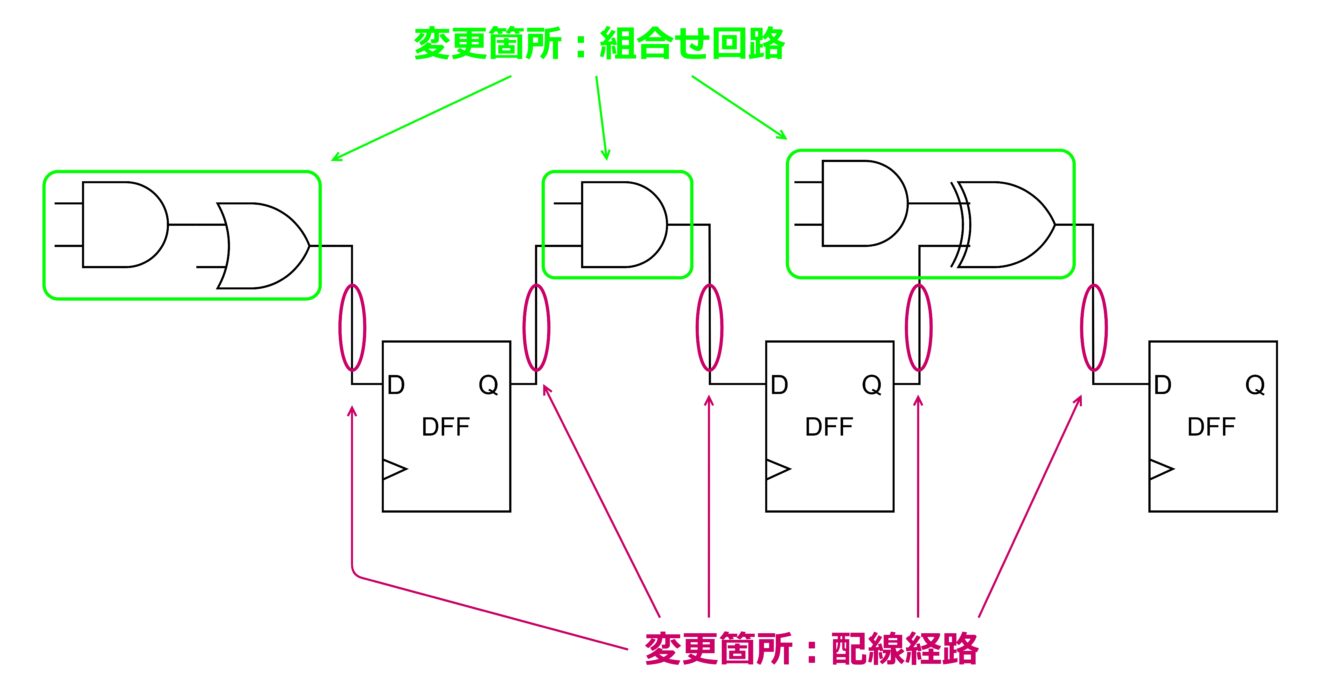
FPGA は、「ルックアップテーブル」という機能を持つ回路を内蔵し、組合せ回路を自在に表現します。また、配線上にたくさんの「スイッチ」を配置し、スイッチを切り替えることで配線経路を変更します。この2つの機能について順番に説明します。
ルックアップテーブルはソフトウェアの分野でよく使われる機能です。まず、全ての入力パターン(入力 ID)に対する出力のパターンを「テーブル」形式の辞書として保管しておきます。そして、パターンが入力される度に辞書の中を探して(ルックアップして)出力を決定するというものです。これは、まさに真理値表の考え方と一致しますので、組合せ回路の機能を表現するのに適しています。真理値表とルックアップテーブルの例を下記に示します。
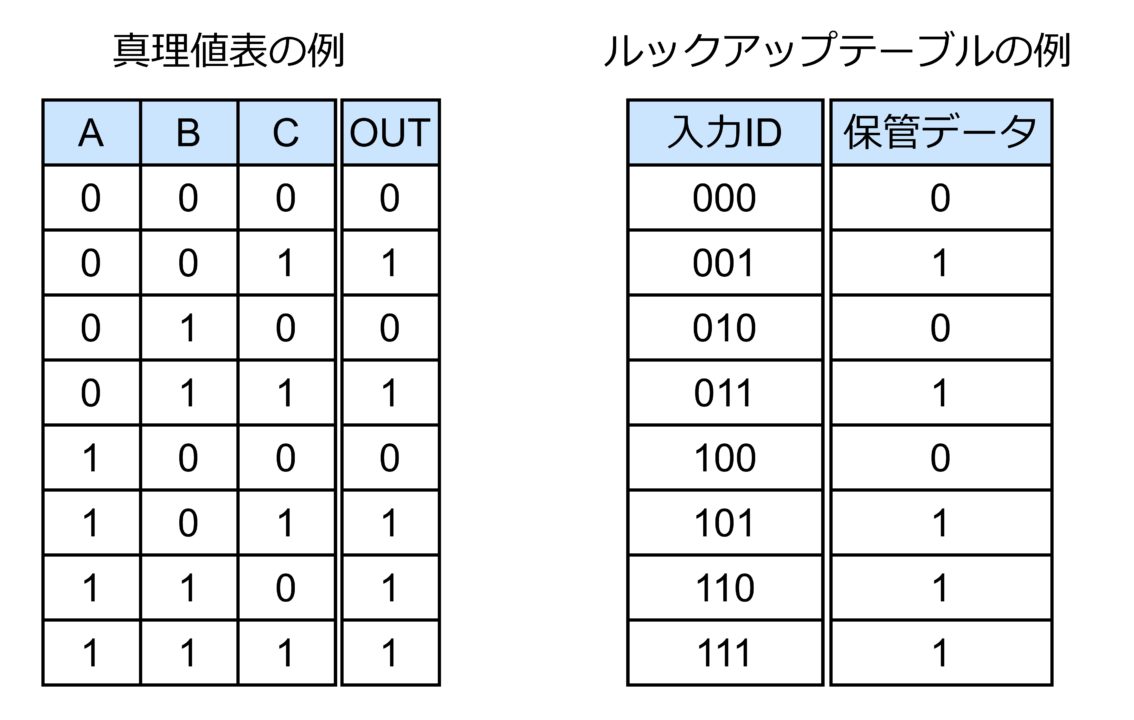
一般的なデジタル回路の設計では、真理値表に対応した回路を作ります。しかしそれでは書き換えることができませんので、FPGA ではルックアップテーブルの回路を内蔵します。ルックアップテーブルの実現の仕方は FPGA 製品によって異なりますが、単純には下図のような回路によって構成可能です。なお、参考のために、上図の真理値表に対応するデジタル回路の回路図も載せておきます。
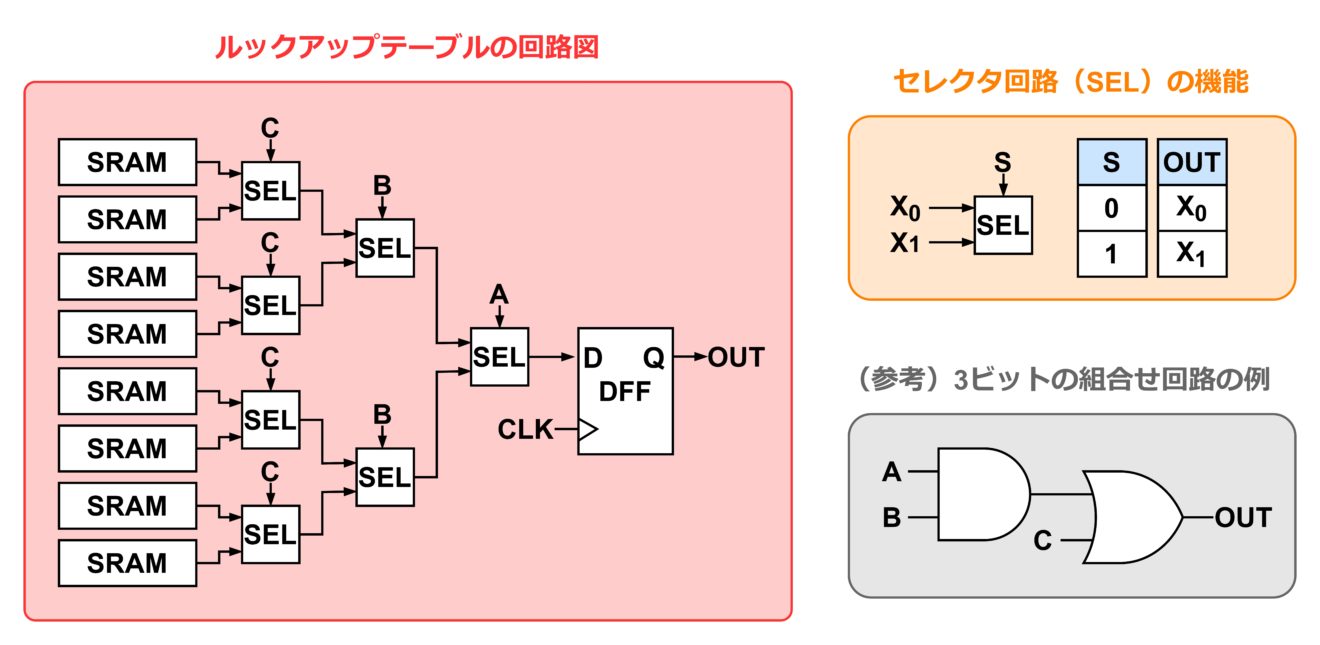
上図は、3bit 入力で 1bit 出力の場合のルックアップテーブルです。前出の真理値表の通り、3bit の組合せは 8 個のパターンになります。つまり、ルックアップテーブルには、8 個の出力パターンを記憶しておくことが求められます。出力は 1bit のため、1bit を 8 個分記憶することになります。これを担うのが SRAM という記憶回路(メモリー素子)です。SRAM を 8 個分用意しておき、入力パターンごとにどの SRAM のデータを出力するかを選択します。
SRAM のデータを選択する機能は、 2 入力のセレクタ回路をトーナメント表のようにピラミッド状に配置することで可能となります。セレクタ回路は、選択信号によって 2 つの入力信号のうちどちらを出力するかを決定するという機能を持ちます。ルックアップテーブルの入力パターンをこの選択信号に接続することで、8 個全ての SRAM にアクセスできるようになります。
また、出力部分には DFF を配置します。デジタル回路はクロック信号に同期して動作するように作るのが一般的で、FPGA 内の回路もそれにならいます。以上が、ルックアップテーブルの大よそのイメージです。
次に、配線経路を変更する「スイッチ」について説明します。スイッチのイメージを下図に示します。なお、これはあくまで「イメージ」で、かなりの部分を省略していることをご了承ください。(実際の回路では、スイッチ単体をトランスファーゲートで作るか、セレクタ回路で作るかという選択肢があります。さらに、複数のスイッチと経路をどのようなトポロジーで組むかを選択する必要があります。)
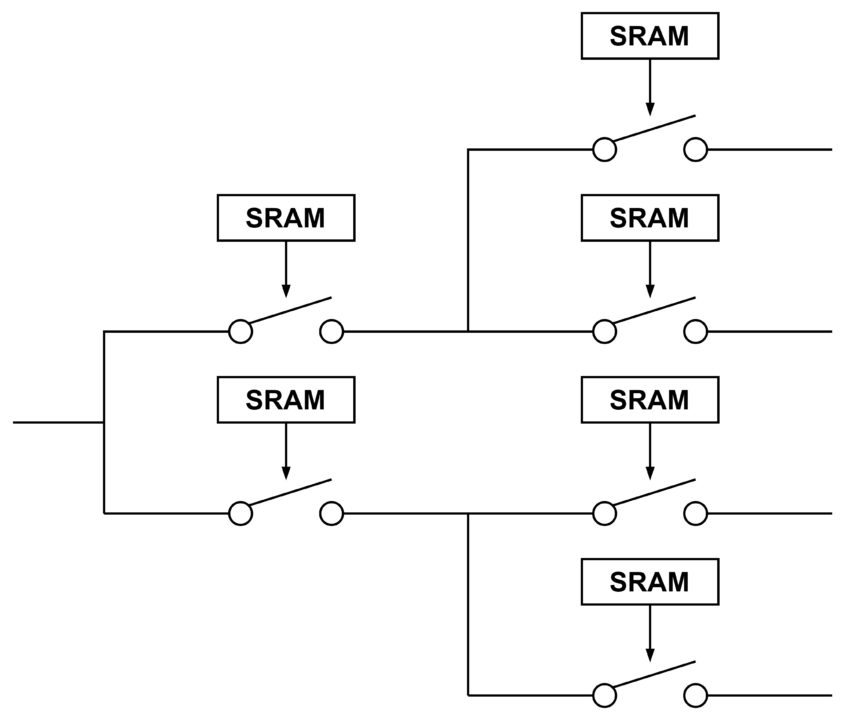
経路の切り替えの選択肢の数に応じて、スイッチを直列に多段に挿入するような構成をとります。スイッチの ON/OFF の情報は SRAM に保存します。なお、原理的にはスイッチの組合せ方によって全ての経路パターンを自在に作ることができますが、現実的には実装面積や信号の遅延時間などの制約も発生します。FPGA メーカーは、経路の自由度と物理的な制約のトレードオフを吟味して、デバイスを開発しています。
FPGA の「書き換え可能なデジタル回路」という機能は、これまでに説明した、ルックアップテーブルと経路切り替え用のスイッチを組み合わせることで実現されます。ルックアップテーブルとスイッチは、それぞれある程度のボリュームごとにブロック化され、FPGA デバイス内に敷き詰められています。イメージ図は下記の通りです。これらのブロックは相互に接続され、ユーザーが指定したデジタル回路として動作します。
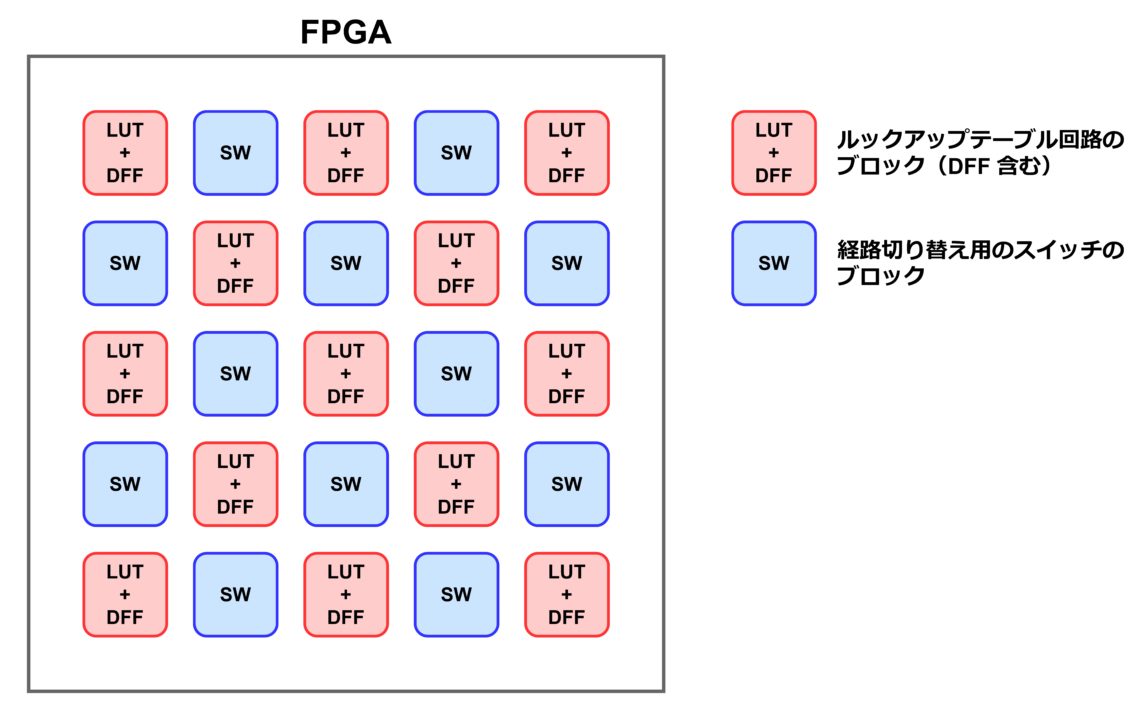
FPGA を使用するユーザーは、書き込みたいデジタル回路の情報を FPGA の専用ツールに入力します。その後、ツール内で「ビルド」と呼ばれる操作を実行すると、ルックアップテーブルとスイッチブロック内の SRAM の状態に応じたバイナリーデータが生成されます。最後に、FPGA に対して何らかのインターフェースを使ってバイナリーデータを書き込めば、FPGA はユーザーが所望するデジタル回路として動作するようになります。
FPGA のメリットとデメリット
CPU・GPU・DSP と比較した場合の FPGA のメリット(長所)は、タイミングが厳しい条件で動かすことができることです。FPGA の中身はデジタル回路ですので、クロックの立ち上がりエッジに同期して動作します。つまり時間精度はクロック周波数の逆数になり、例えば 250MHz のクロック周波数では時間精度は 4ns になります。CPU もリアルタイム OS を搭載することで通常の OS よりもかなり時間精度を高めることができますが、せいぜい数 us か数百 ns オーダーでしょう。また、リアルタイム OS はあくまでソフトウェアによる制御になりますので、指定した時間内に処理が終わらないこともあります。間に合わないリスクを出来るだけ排除したいのであれば、時間精度の高低によらず FPGA を選択するのがおすすめです。
CPU・GPU・DSP と比較した場合の FPGA のデメリット(短所)は、設計が大変だということです。FPGA の機能の設計は、デジタル回路の設計手法にのっとります。近年のデジタル回路設計は、通常の LSI の設計も FPGA 向けの設計でも Verilog-HDL や VHDL といった HDL(RTL)と呼ばれるプログラミング言語を使って行います。HDL は「Hardware Description Language(ハードウェア記述言語)」の略称で、RTL は「Register Transfer Level(レジスタ転送レベル)」の略称です。両者はどちらも Verilog-HDL と VHDL を合わせた総称として使われ、技術者の間ではだいたい同じ意味の言葉として使われています。
CPU・GPU・DSP の機能も C 言語などのプログラミング言語によって記述されますが、C 言語は抽象度が高いため、とりあえず動くコードを記述するためのハードルは HDL に比べると格段に低くなります。言い換えると、HDL は最低限の動作をするためのコードを書くために比較的高度な知識が必要になるということです。たとえプログラミング言語で記述するにしても、デジタル回路の信号線やクロックレベルのタイミングを厳密に表現する必要があることに変わりはありません。System-C 等の HDL よりも抽象度が高い高位言語というプログラミング言語も存在しますが、回路の機能や仕様によっては使えない場面が多いのが現状です。また、高位言語を使いこなすためにはやはりデジタル回路設計の技術が求められます。デジタル回路の設計はソフトウェアの設計よりも入口の難易度が高いことから FPGA の設計は大変です。
さらに、熟練の技術者であっても、デジタル回路の設計はソフトウェアの設計よりも長い期間がかかります。電気信号の動きを細かく記述しないといけないため仕方がないことです。土俵が異なるので一概に比較できませんが、設計期間に 10 倍くらいの差が生じることもありえます。以上のように、設計の入口のハードルが高いことと、設計期間が長くなることから「FPGA の設計は大変」です。
次に、普通のデジタル LSI(SoC)と比較します。この場合の FPGA のメリットは、所望の機能を動作させるまでにかかる時間が短いことです。LSI の開発では、設計と製造にそれぞれ少なくとも数ヶ月かかります。つまり、実現したい機能を着想してから実機での動作が確認できるまで 1 年くらいは待たないといけません。一方で、FPGA では早ければ数日程度で動作確認まで進むことができます。回路設計のフローは、LSI 設計と FPGA 設計でそこまで大きくは変わりません。いずれも HDL を使ってプログラミングを行い、シミュレーションを実行して機能を確認します。ただし、FPGA は何度でも機能を書き換えることができるために多少の設計ミスが許されることから、LSI 設計に比べてシミュレーション等の検証の工程を短縮することができます。また、機能によってはシミュレーションを省略して実機で動作確認してしまうこともありえます。
さらに、FPGA メーカーが様々な IP を用意してくれていたり、専用のツールがインターフェースの部分の記述を補ってくれたりしますので、設計期間もかなり短縮できることが多いです。また、独自に LSI を製作した場合には動作確認用の電子基板(ボード)も自分で作らないといけないですが、FPGA は開発用のボードが市販されている点も有利です。
LSI と比較した場合の FPGA のデメリットは2つあります。1つ目はスピードと消費電力といった性能が劣ることです。前述のルックアップテーブルの回路図で示したように、書き換え可能なデジタル回路という機能を実現するために、FPGA 内の回路は普通のデジタル回路よりも複雑になります。同じ図の右下に示した組合せ回路の例と比較すると、一目瞭然です。同じ機能を複雑な回路で表現しますので、結果的に回路の動作速度は遅くなり、消費電力も大きくなります。速度については、同じ世代の半導体プロセスで製造した LSI と FPGA を比べると、FPGA で実現可能なクロック周波数は LSI の数分の 1 になります。(例えば、LSI ⇒ 4 GHz、FPGA ⇒ 1GHz のような対応関係。)
2つ目のデメリットは、デバイス1個(1チップ)あたりのコストが高いということです。半導体のコストは、設計コスト、製造コスト、販売管理コストの組み合わせで決まり、単純な計算は難しいところです。それでも、回路が複雑になればチップ面積が大きくなって製造コストは確実に高くなるということは断言できます。ざっくりとしたイメージですが、同じような機能のデジタル LSI と FPGA で比較すると、例えば LSI が1個数千円から数万円になる場合、FPGA は1個数万円から数十万円になります。民生品の中では単価が高い自動車であっても、部品に数十万円の FPGA を採用することには躊躇してしまいます。
以上のように、FPGA にはメリットとデメリットがあって、状況に応じて使い分けることになります。デジタル回路なのに書き換えができるという便利さから、ロボット、自動車、航空、宇宙を始めとした様々な用途で活用されています。一方で、設計が大変な割には性能が低いことから、特に民生品の分野ではあまり普及していないことも事実です。Xilinx や Intel 等の FPGA メーカーには、設計の難易度を下げ、デバイスの性能を上げるための一層の努力が求められます。FPGA を採用するのは簡単ではありませんので、必要になった際には、まずは専門の技術者に相談することをおすすめします。
AI 専用 LSI
ロボット向けのプロセッサーを選択する際に、CPU、GPU、DSP、FPGA に加えて AI 専用LSI も重要な候補になります。AI 専用 LSI は、色々なメーカーが様々な機能のものを開発していますが、その多くはニューラルネットワークの処理を効率的に実行することが目的になっています。
ロボット向けにニューラルネットワークが使われる用途として最も多いのは画像認識でしょう。画像認識を目的としたニューラルネットワークは CNN(Convolutional Neural Network)をベースとします。AI 専用 LSI は CNN に特化した回路を内蔵することで、CPU や GPU などの汎用性の高いプロセッサーよりも高速もしくは高効率な処理を可能にします。繰り返しになりますが、AI 専用 LSI には実に様々な種類のものが存在します。次項以降にて、筆者の独断と偏見でざっくり3つのタイプに分けて紹介します。なお、AI 専用 LSI には「学習」に対応するもの、「推論」に対応するもの、両方に対応するものがありますが、ここでは推論のみに対応したものを想定することにします。また、いずれのタイプでも CPU が一緒に内蔵されていて CPU が全体の処理をコントロールしているものと思ってお読みください。
タイプ1:CNN 全体をそのまま回路化
1つ目は、CNN 全体をそのまま固定のデジタル回路として LSI に実装するというタイプです。つまり、普通のデジタル回路として普通に載せる、というやり方です。この方法ですと、プロセッサーで命令を読み込んだり結果をレジスタに格納したりする際に生じるオーバーヘッドをゼロにすることができますので、高速に処理できて電力効率も高くなります。ただし、固定の回路なので、後で計算内容を変更することはできません。
一口に画像認識向けの CNN といっても、入力の画像サイズや出力(つまり認識結果)のフォーマットによって CNN の形状は変わります。さらに、必要な精度によってレイヤーの「段数」や各段の特徴量方向の次元数が異なります。このタイプで製造してしまうと、後で CNN の形を変更することは不可能なのです。どういった用途にも耐えうる CNN の形状というものは存在しませんので、このタイプの LSI をそのまま一般販売してもおそらくほとんど売れないでしょう。
それでも、LSI を搭載する最終製品やモジュールが決まっていれば、選択する価値があります。例えば、ソニーなどが作っている画像認識機能付きのCMOS イメージセンサーが挙げられます。ピクセル数や認識機能、精度などの仕様が決まっていますので、CNN は固定でもかまいません。
なお、計算内容(計算グラフ)は固定でも、重み係数のセットだけを外部から書き換えられるようにして部分的に機能をアップデートできるようにしているケースもあるようです。例えば、人の顔を見分ける機能から、ミカンやリンゴなどの一般的な物体の種類を見分ける機能に切り替えるようなイメージです。
タイプ2:頻出する計算グラフ単位で回路化
2つ目は、CNN の中で頻出する計算グラフをいくつかピックアップして回路化する、というタイプです。例えば Convolution 層に含まれる 3 ピクセル × 3 ピクセルの積和演算を 1 つの要素回路として実装しておくようなイメージです。このような要素回路を順番に実行することで CNN 全体の計算内容を満たします。こういう仕組みにすることで、製造後にも CNN の形状を変更できるようになります。
このタイプは、CPU、GPU、DSP と同様にプロセッサーの一種に位置づけられます。ざっくり言うと、CPU 内の ALU を要素回路で置き換えたような構成になります。CNN を事前に専用のコンパイラによって命令のリストに変換しておいて、命令のリストの順番で要素回路を実行していきます。AI 専用 LSI では CPU 等に比べて要素回路の規模が大きいため、命令の個数が少なく、プロセッシングのオーバーヘッドも小さくなります。その分だけ従来型のプロセッサーよりも高速で低消費電力にすることが可能です。
タイプ1に比べると処理速度と電力効率は劣りますが、CNN を変更できるというメリットを持ちます。ただし、予め実装してある要素回路しか対応できないという制約もあります。例えば RNN(Recurrent Neural Network)のようなフィードバック経路を持つニューラルネットワークに対応していない、といったケースが考えられます。対応していないネットワークが含まれる場合、LSI 専用に用意されているツール(コンパイラ等)によって処理のされ方は異なりますが、ビルドの段階でエラーになったり、対応していないネットワークの部分だけ CPU で計算するようになっていたりします。
なお、タイプ2には例えばルネサスエレクトロニクスの「DRP」が該当するのではないかと思います。
タイプ3:行列計算単位で回路化
3つ目のタイプは、要素回路を行列単位にしたプロセッサーです。例えば Google の「TPU」が該当すると推測されます。行列単位という点では GPU と同じコンセプトになります。異なるのは、演算回路のビット幅と数値の型です。GPU の演算回路は主に 16 ビットもしくは 32 ビットの浮動小数点型に対応したものになります。一方で、このタイプの LSI では、一般的な CNN で必要な計算精度に合わせて 8 ビットや 16 ビットの整数型の演算回路を使うことが多いようです。ビット幅が小さくて整数型であることから演算回路がコンパクトになりますので、デバイスの価格を抑え、電力効率を高めるという効果が狙えます。また、条件によっては処理速度も上がります。
タイプ2に比べて要素回路が細かくなりますので、対応できる CNN の範囲が広がります。一方で、処理速度という点では GPU とそれほど変わらないため、cuda 等のソフトウェアが充実している分だけ NVIDIA の GPU の方が開発しやすくて良いかもしれません。
補足
ここでは、AI 専用 LSI を要素回路の規模で分類して3つのタイプに分けました。一方で、実際に CNN の計算の高速化を考えた際には、演算速度だけではなく、データの通信速度がボトルネックになりえます。演算が速くても、演算に必要なデータが演算回路に届かない限り処理を開始することができないのです。特に規模の大きなニューラルネットワークを実行する際に、通信速度がネックになるケースが増える傾向にあります。
ニューラルネットワークの計算を分解していくと、次のような数式にたどり着きます。
$$y_i = \sum_{j} (w_{ij} \cdot x_{ij} ) + b_i$$
x が入力値で、y が出力値です。w は重み係数、b はバイアスと呼ばれ、それぞれディープラーニング等の機械学習によって決定されます。ニューラルネットワークは膨大な数の数式によって構成され、w と b もその数式の数分だけ存在します。つまり、ニューラルネットワークの規模を大きくしていくと w と b の個数がどんどん増えていき、例えば 1GB くらいになることもありえます。入力が画像データの場合、データサイズは大きくても数十 MB 程度ですので、w と b のデータ量の方が入力データよりも大きくなることがあり得る訳です。
w と b は機械学習が終わった段階で固定化されますので、推論実行時には「定数」という扱いになります。それでも、CPU や GPU などの汎用のプロセッサーでは、入力値の x と定数の w と b を別の扱いにすることは難しく、演算を実行する度にメインメモリから演算回路へ転送する必要があります。(キャッシュされれば、多少は高速化できますが。)
一方で AI 専用 LSI の場合、入力データと定数データの扱いを分けるように回路を実装することがあります。演算の順番がコントロールされていますので、定数が使われる順番も予め把握することができます。このことを利用して、定数データを別途「整理された効率的な通信経路」を通るような回路構成にすることもあるのです。本当は、定数を全て LSI 内の SRAM に格納してしまうのが理想ではありますが、1GB とかの SRAM を搭載するのはレイアウト面積的に困難なので、現実的には SRAM と整理された通信経路の合わせ技で対応することになります。
以上のように、AI 専用 LSI は、演算の要素回路の規模だけではなく、定数データの保管と通信の仕方によっても特徴づけられるということを補足しておきます。
